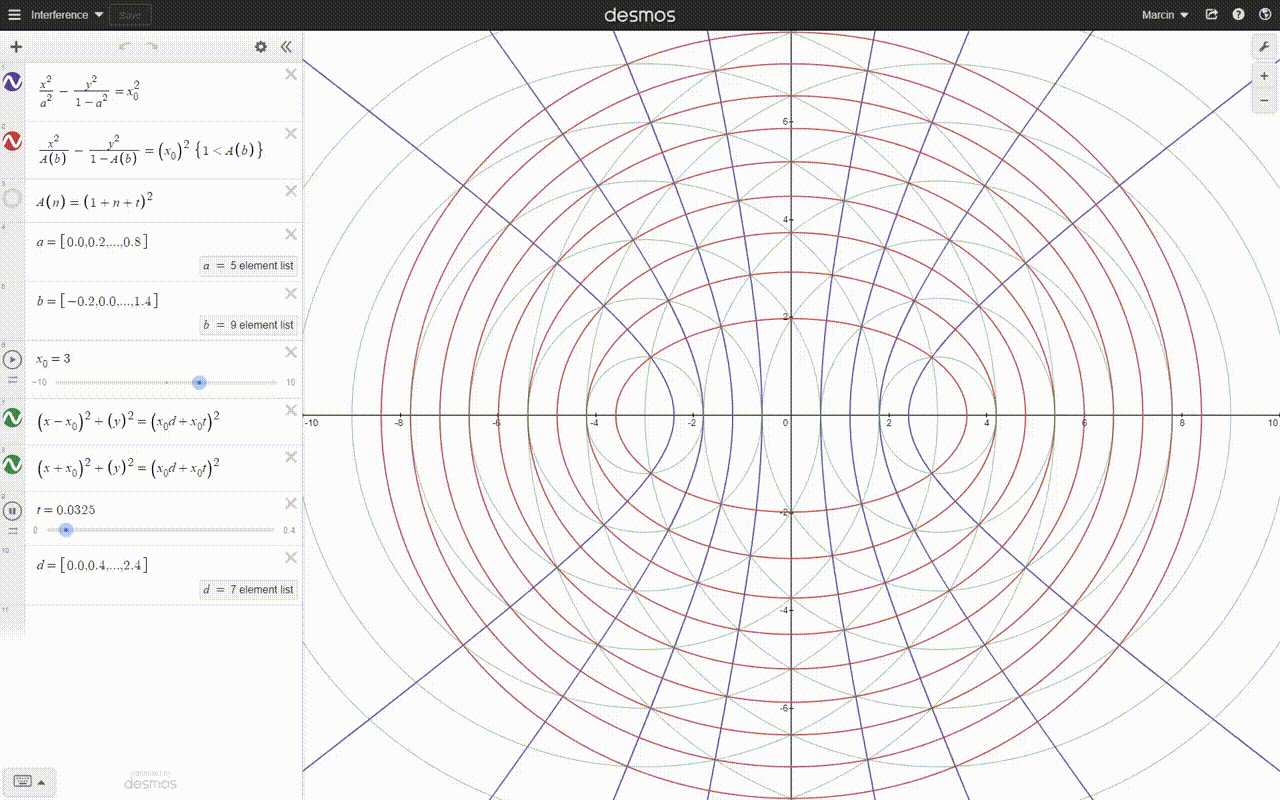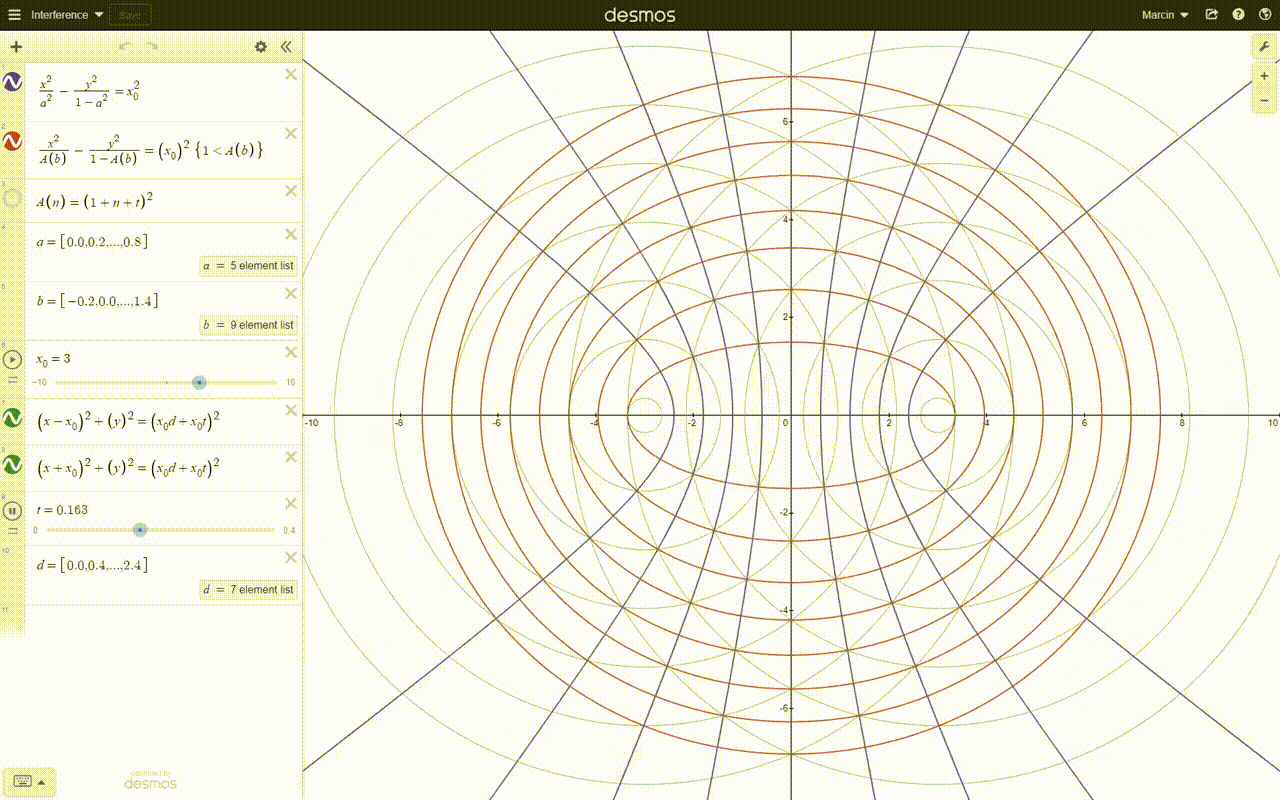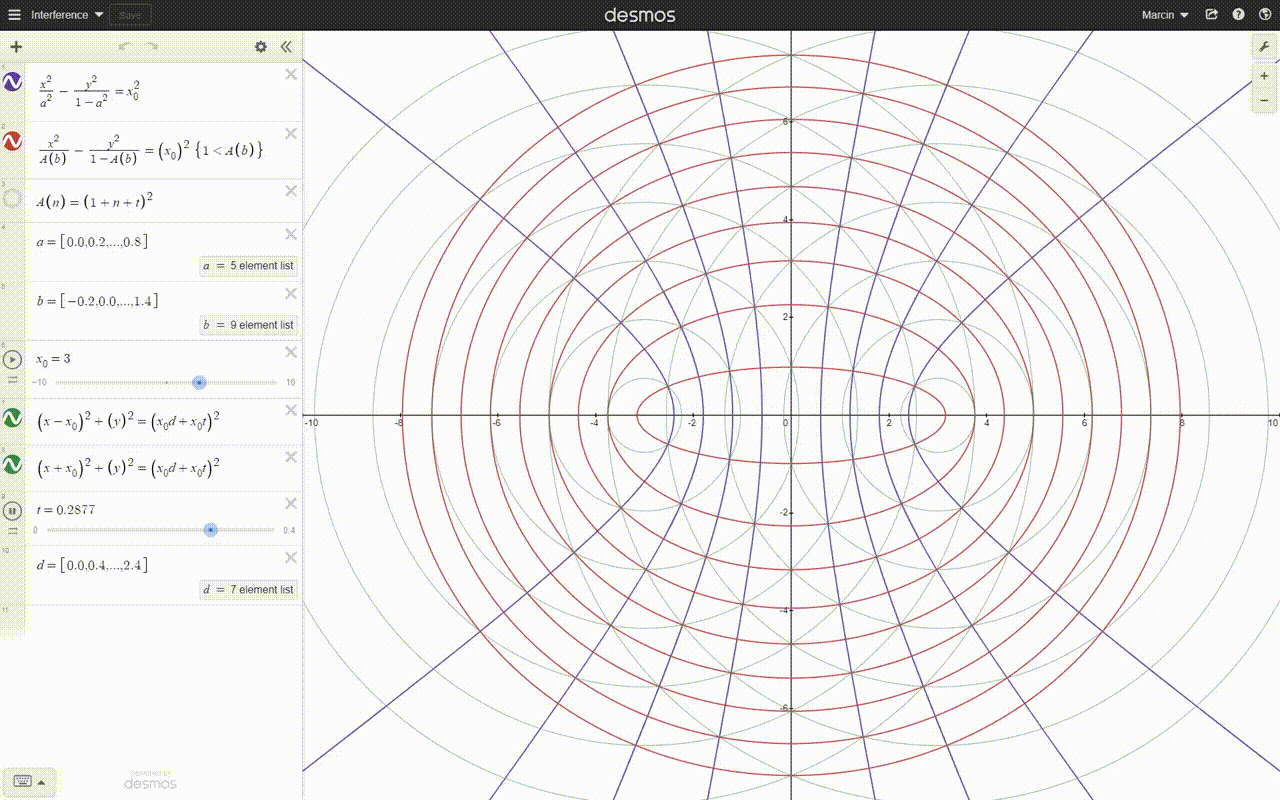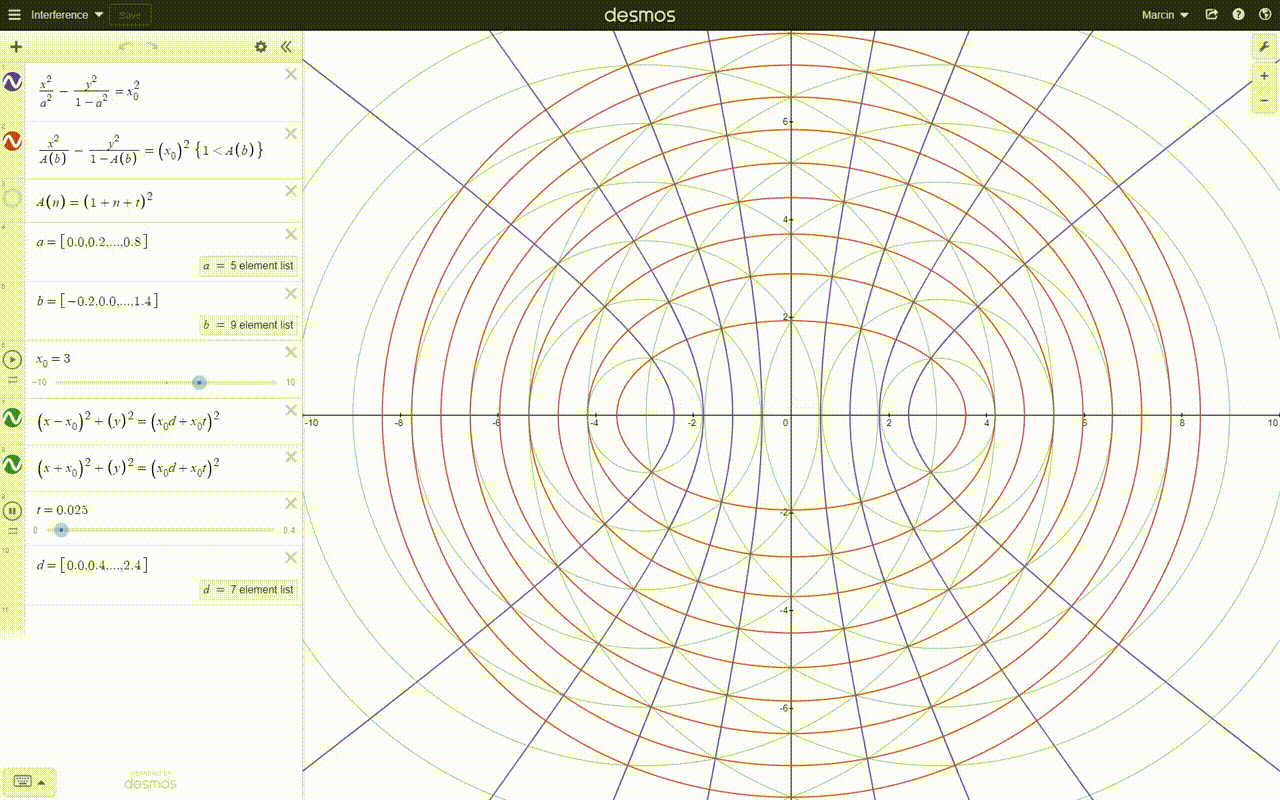
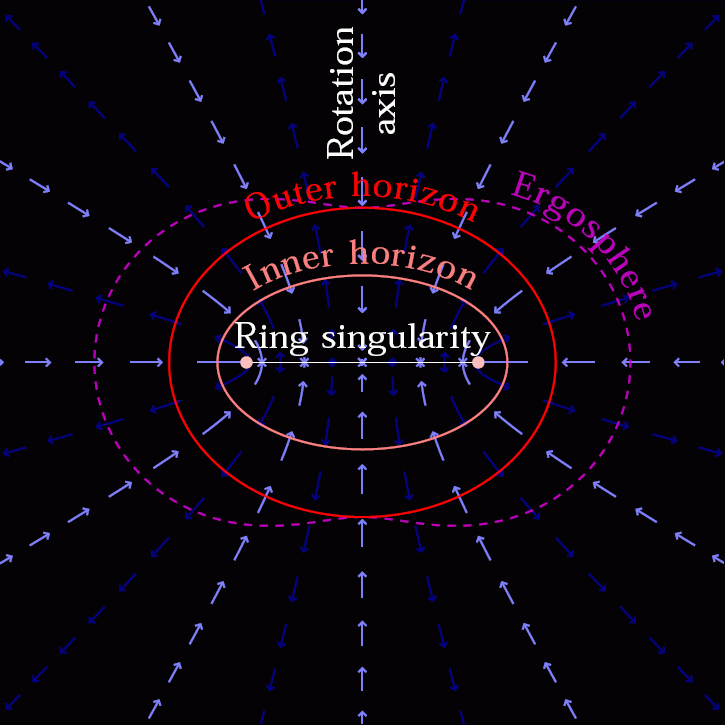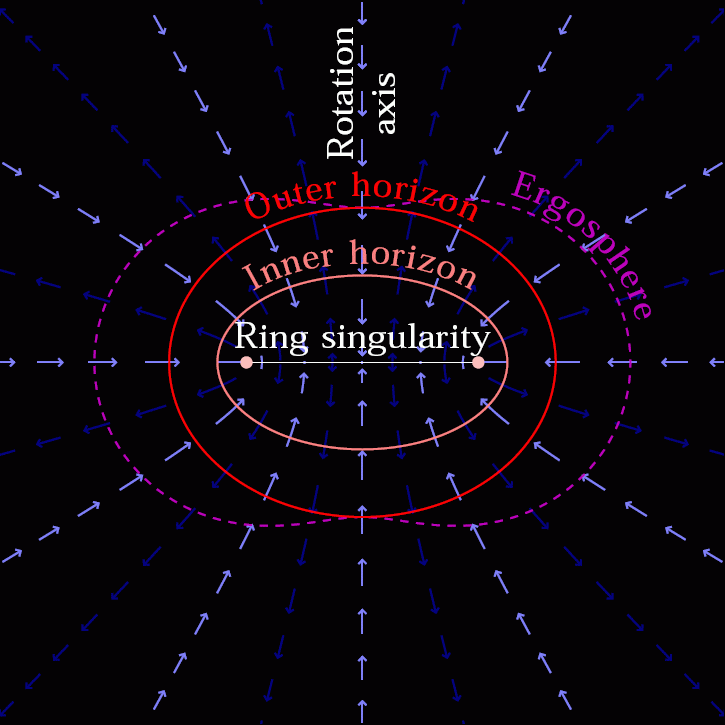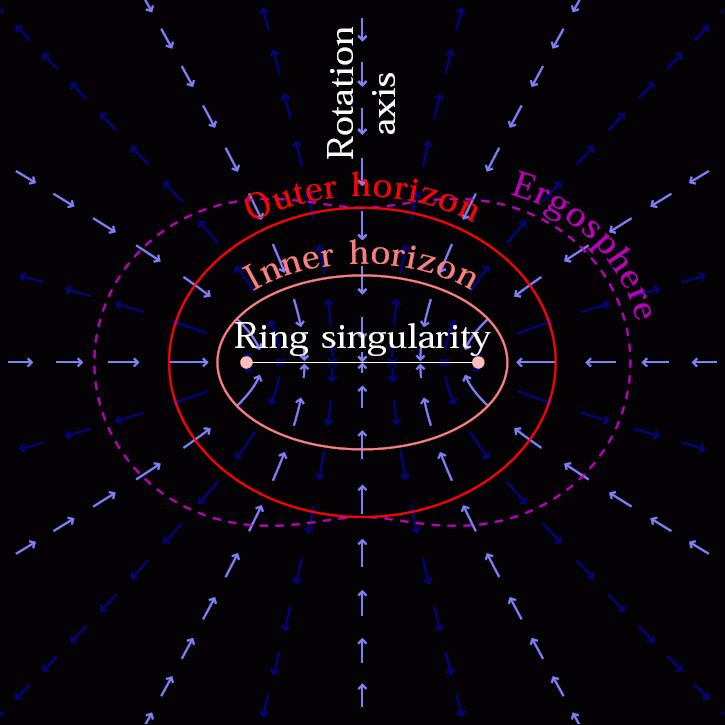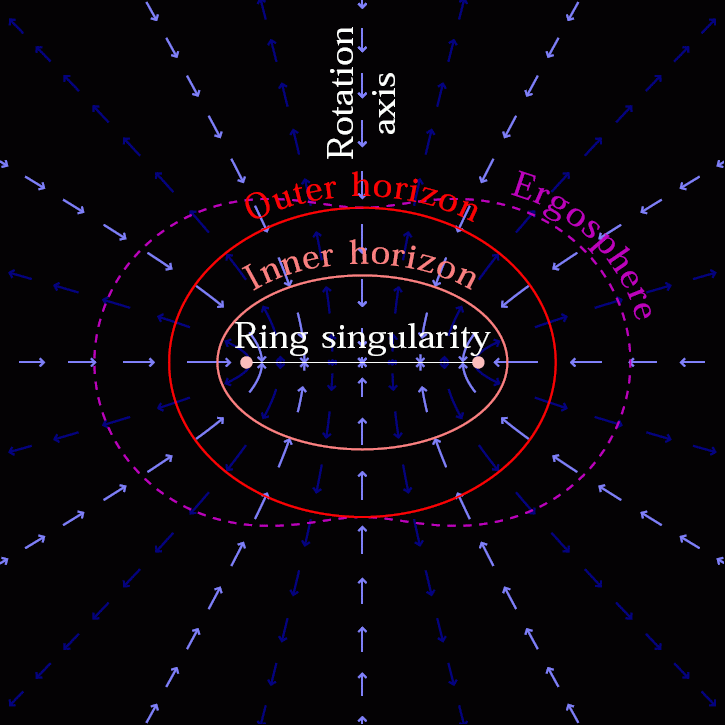
Hyperbolas have the same equation as ellipses and transition to each other. The only difference is the sign of the second component with y^2, when the denominator becomes negative because t^2 becomes > 1.
Hyperbolas and the ellipses crossing them at right angles are created by the interference pattern of two overlapping spherical fields or spherical waves. Hyperbolas and ellipses are geodesic curves of our space-time, and small bodies move along them near large bodies, passing them in hyperbolas or orbiting them in ellipses. However, they do not describe the trajectories leading to the collision.
Mindfuck: Each point in space-time, whether flat or curved, has its own space-time hyperbola in (dt, dr) coordinates as opposed to ordinary pure-space hyperbolas and ellipses which are mere (x, y) trajectories. Each spacetime hyperbola at each point determines, first of all, the rate of time flow and the density of space at that particular point, but not only. It also tells how these parameters will change at this point depending on the speed of a small body passing through this point, the mass of which I am neglecting in this consideration. If it were large, it would change the shape of the hyperbola itself. The greater the velocity of a body, the further from the origin of the coordinate system the point (dt, dr) will be located on the hyperbola curve, defining the rate of time and the density of space at this point.
Moving through space-time, the body jumps from one spacetime hyperbola to the next, because each place has its own. However, it cannot jump from a specific point (dt, dr) of one curve to any point on the next one. It must jump to a point that corresponds to its speed at that point. It so happens, that the spacetime trajectory of the body intersects at right angles the plane of successive spacetime hyperbolas, being tangential at the point of intersection to the surface of their hyperboloids. This trajectory maximizes the passage of time and minimizes the space traveled, i.e. the distance. This can be called moving on a gradient of the passage of time or the density of space.
As for the picture or the animation, I doubted it. Too many hyperbolas and dimensions.
Teaser
Lorentz transformation invariant has hyperbola equation:
ds^2 = (cdt)^2 - (dx)^2
although I prefer this form:
ds^2 = (cdt)^2 - (vdt)^2 Hyperbolas, rotated by 45 degrees, give us (cdt)*(vdt) = const or dt*dx = const equations. These are actually y = 1/x, no kidding :) And they look like this:
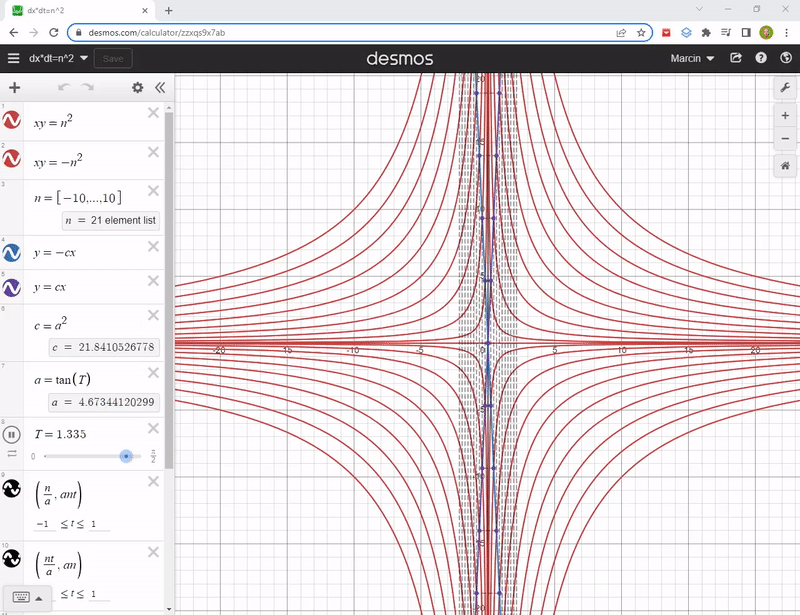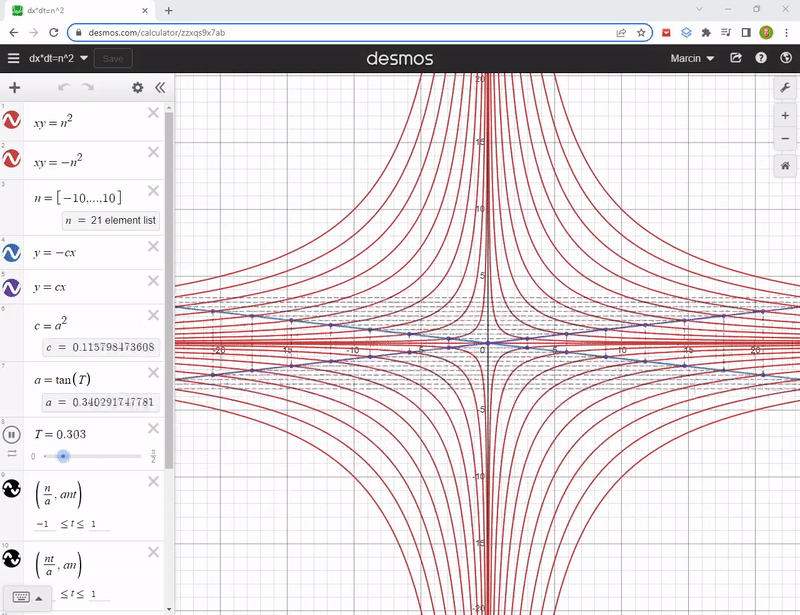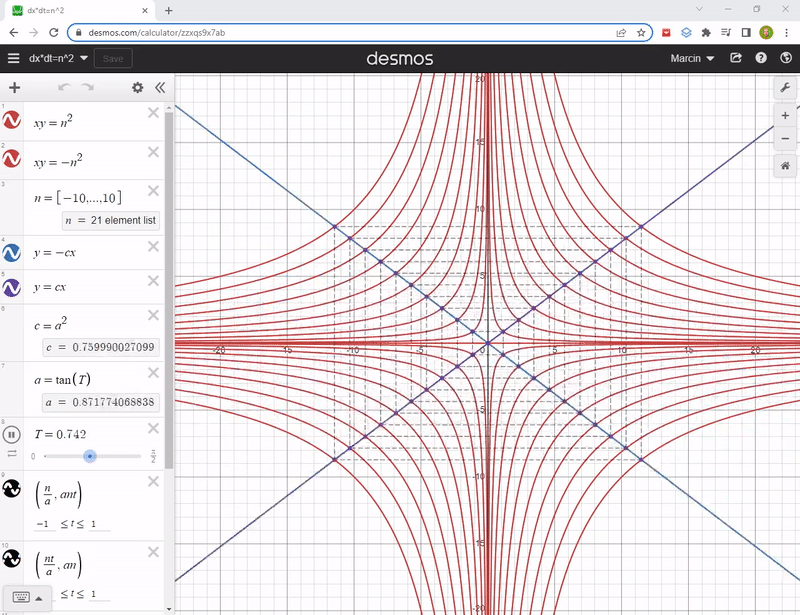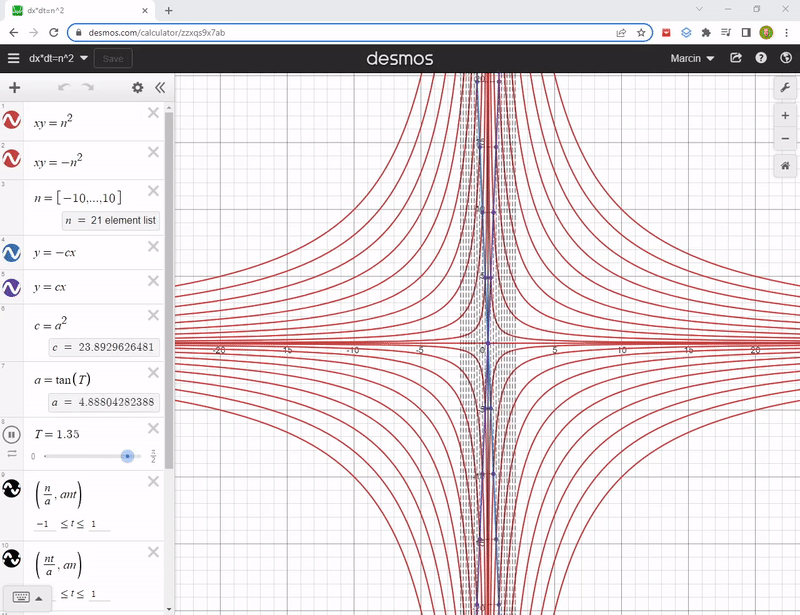
The explanation of stretched rectangles that are spanned on rotating axes will probably not come in the future post, although I have it in polish.